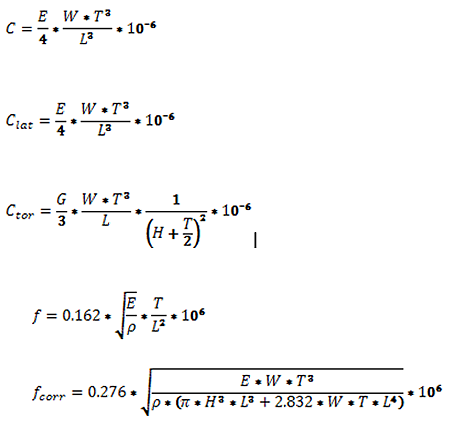Selecting the correct AFM cantilever is critical for the success of an Atomic Force Microscopy measurement. The geometric dimensions of an AFM cantilever determine its mechanical properties such as oscillatory resonances and stiffness. In turn, the mechanical properties determine the application mode for which the AFM cantilever is suitable. There is no strict definition on the exact force constant values that make an AFM cantilever stiff (hard), intermediately stiff or soft. The values below are according to our own definitions.
Thick and short AFM cantilevers usually have high resonance frequencies and high force constants* >40N/m. These stiff AFM cantilevers allow maximum scanning speeds in non-contact or intermittent contact mode AFM operation.
» Browse AFM probes with tapping mode AFM cantilevers
AFM cantilevers with intermediate lengths and intermediate thicknesses have intermediate resonance frequencies and intermediate force constants in the range 3-15N/m. These intermediately stiff AFM cantilevers are usually preferred for soft intermittent contact mode AFM measurements with reduced tip-sample interaction (5-15N/m) and for force modulation measurements (3N/m).
» Browse AFM probes with soft tapping mode AFM cantilevers
» Browse AFM probes with force modulation AFM cantilevers
Long and thin AFM cantilevers have low resonance frequencies and low force constants <1N/m. The soft AFM cantilevers allow high sensitivity contact mode and Lateral Force Microscopy (LFM) AFM measurements.
» Browse AFM probes with contact mode AFM cantilevers
There are some AFM cantilevers whose geometric dimensions deviate from the general rules in order to fulfill special system or application requirements. For example, certain AFM systems require » long tapping mode AFM cantilevers, while other AFM systems require » short contact mode AFM cantilevers. There are technological limitations as to what AFM cantilever shapes can be manufactured reliably and reproducibly.
For more information on AFM cantilevers, please contact us.
* We are referring to the normal force constant of the AFM cantilever. For more information about the different AFM cantilever force constants, check the next chapter.
The normal resonance frequency (or simply the resonance frequency) f of an AFM cantilever refers to the resonance frequency for small amplitude oscillations in the direction normal to the sample facing surface of the AFM cantilever. The calculations for this parameter below neglect the mass of the AFM tip.
The corrected resonance frequency fcorr of an AFM cantilever takes the AFM tip mass into account. Here, the AFM tip is modeled as a cone with height H and a base diameter H.
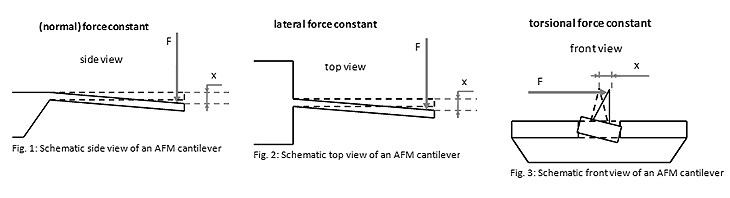
The normal force constant (or simply the force constant) C of an AFM cantilever is the ratio of the applied force from the top or the bottom side at the free cantilever end to the free end’s displacement for small displacements (Fig. 1). This force constant is most relevant for determining the tip-sample interaction during the majority of AFM operation modes.
The lateral force constant Clat of an AFM cantilever is the ratio of the applied force from the side at the free end of the AFM cantilever to its displacement for small displacements (Fig. 2).
The torsional force constant Ctor of an AFM cantilever is the ratio of the applied lateral force at the AFM tip to the lateral displacement of the AFM tip for small displacements (Fig. 3).
The calculator below calculates important parameters of silicon AFM cantilevers based on their geometric dimensions.
f [kHz] – resonance frequency of the AFM cantilever (neglecting tip mass)
fcorr [kHz] – resonance frequency of the AFM cantilever taking tip mass into account
C [N/m] – (normal) force constant of the AFM cantilever
Clat [N/m] – lateral force constant of the AFM cantilever
Ctor [N/m] – torsional force constant of the AFM cantilever
T [µm] – AFM cantilever thickness
W [µm] – AFM cantilever width
L [µm] – AFM cantilever length
H [µm] – AFM tip height
ρ = 2.33g/cm3 = 2330kg/m3 - density of silicon
E = 1.69*1011 N/m2 - modulus of elasticity / Young’s modulus in the <110> direction of silicon
G = 0.5*1011 N/m2 modulus of rigidity / modulus of elasticity in shear of silicon
The calculator calculates the resonance frequencies and the force constants according to the following formulas: